Cryptography in Elixir using Rustler

I recently started learning Rust and I didn't wait long to try writing a NIF library for Elixir. My toy project block_keys is using a C NIF for the libsecp256k1 library used to create Bitcoin (and similar) PKI and also sign transactions. Parity wrote a pure Rust implementation of libsecp256k1 and this seemed like the perfect opportunity to try writing an Elixir wrapper around that.
Why do we need Rust
Generating Public / Private keys for most blockchains uses Elliptic Curve Cryptography (ECC). Libsecp256k1 is a elliptic curve that was first used for Bitcoin. I won't go in depth into ECC but in simple terms we have a math function that defines the curve with some default parameters specific to the libsecp256k1 curve. Generating a Public Key given a Private Key for example is achived by doing a point addition on the curve. Similarly, generating the Private Key is a point multiplication using some randomness and a very large prime number. I suspect that there aren't any pure Elixir implementations of libsecp256k1 for this reason: the language wasn't optimized for those kind of large number computations.
Rustler
Rustler is an Elixir package that saves us from a lot of boilerplate code required to write a Rust based Nif. According to the library, the Rust code you write should never be able to crash the BEAM.
I decided to write this post because, after going through a few blog posts about Elixir and Rustler I still couldn't figure out how to return a binary from Rust to Elixir. Most of the examples showed either simple integer, strings or maps return values. In order to make my crypto port work I needed to figure out a way to return a Rust data structure that would in turn be converted to an Elixir binary.
If you want to skip ahead and check out some code you can access the repository at github.com/tzumby/rusty_secp256k1/. Be warned that I'm still learning Rust and this is probably not safe to use in production.
Setting up Rust in a new project is super straight forward so I won't go into that here. There is one gotcha if you're publishing a Rust based hex library: you need to define all the files you want to include in your mix.exs
defp package do
[
maintainers: ["tzumby"],
name: "rusty_secp256k1",
licenses: ["Apache License 2.0"],
links: %{"GitHub" => "https://github.com/tzumby/rusty_secp256k1"},
files: [
"mix.exs",
"native/secp256k1/src",
"native/secp256k1/Cargo.toml",
"lib",
"LICENSE",
"README.md",
"CHANGELOG.md"
]
]
end
Make sure you do that, otherwise as soon as you try to import this library in a Mix project, the rustc compiler won't be able to find the native folder in there unless you specify it.
Returning a binary from Rust
Rustler provides an OwnedBinary class (meaning it's mutable). We need to initialize that binary and give it a size in bytes. In the following snippet we're exporting a 33 bytes Public Key.
In the next line we convert the Public Key to a slice (a sized vector), after which we copy it into the OwnedBinary we defined earlier. Finally we release the binary (making it immutable) and return it.
let mut erl_bin: OwnedBinary = OwnedBinary::new(33).unwrap();
let public_key_serialized = public_key.serialize_compressed();
erl_bin.as_mut_slice().copy_from_slice(&public_key_serialized);
Ok((atoms::ok(), erl_bin.release(env)).encode(env))
Elixir binary argument
To accept a binary as an argument is even easier. All we have to do is decode the argument and cast it to a Binary.
let public_key_binary: Binary = args[0].decode()?;
Using the library
Let's start a new mix project and add the rusty_libsecp256k1 as a dependency:
defp deps do
[
{:rusty_secp256k1, "~> 0.1.6"}
]
end
Now drop into an iex session and let's use the three functions we wrote wrappers for. The first creates a Public Key given a Private Key. The Private Key is a 32 byte random binary, the second required parameter is the Public Key type (:compresseed vs :uncompressed)
iex(1)> {:ok, public_compressed = RustySecp256k1.ec_pubkey_create(:crypto.strong_rand_bytes(32), :compressed)
iex(2)> {:ok,
<<2, 35, 243, 177, 200, 204, 115, 180, 14, 144, 73, 221, 179, 178, 12, 56, 129, 76, 185, 101, 197, 149, 183, 149, 26, 99, 146, 36, 95, 46, 234, 26, 10>>}
Keys in ECC are points on the curve and have X and Y coordinates. A compressed Public Key consists of just one of the coordinates and reduces the size (we can compute the full uncompressed key given just one of the coordinates)
iex(3)> RustySecp256k1.ec_pubkey_decompress(public_compressed)
{:ok,
<<4, 93, 124, 236, 18, 198, 10, 55, 81, 140, 223, 165, 236, 66, 44, 244, 229, 143, 40, 223, 225, 107, 136, 132, 28, 234, 146, 147, 133, 244, 9, 18, 163, 127, 209, 66, 4, 137, 148, 155, 186, 48, 28, 142, 142, 142, 227, 3, ...>>}
The uncompressed public key has 65 bytes while the compressed key has 33 bytes. Both Bitcoin and Ethereum addresses are created from compressed public keys.
Finally, one of the key operations that allows Hierarchical Deterministic wallets to generate a very large number of addresses starting from an initial seed, is the tweak add operation. This is kind of like the addition operation in math, but because we're using an elliptic curve and working in mod p, it's a little different.
As you can see in the diagram below, we use a parent Public Key, do an HMAC-SHA512 hashing and tweak add with the same key (the green + sign).
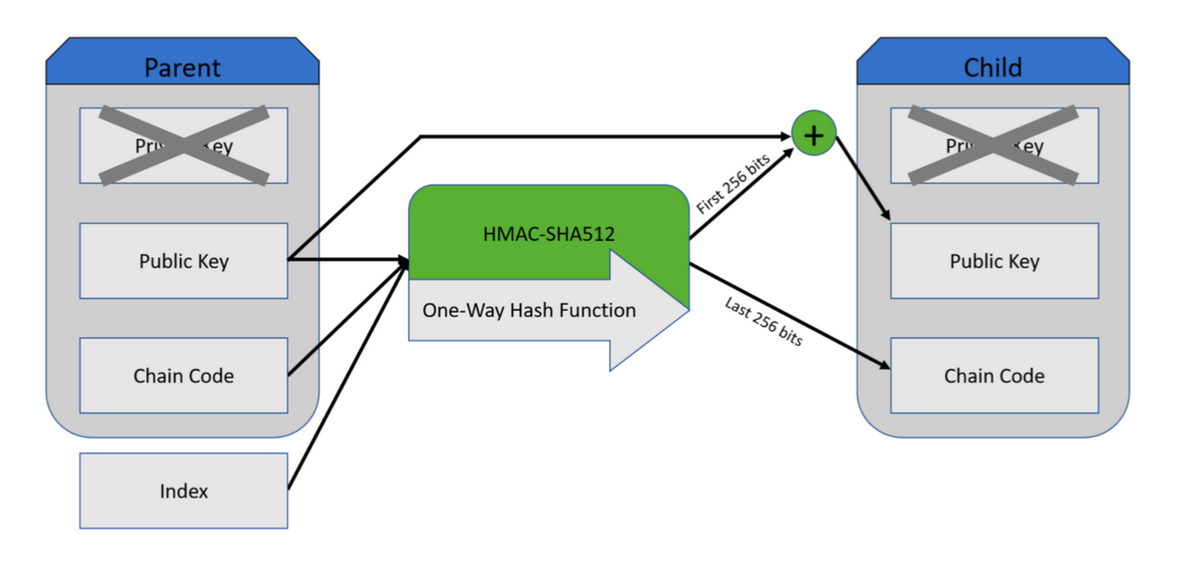
If you'd like to learn more about HD wallets you should check out the BIP 32 document. I also worked on a cheat sheet that explains the standard.
Member discussion